I. Решите задачи.
N1. На шхуне капитана Врунгеля "Победа" (а потом "Беда") был четырехзначный номер.
Номер был примечателен тем, что являлся квадратом целого числа. Во время шторма смыло первую цифру,
и номер стал кубом целого числа. После следующего шторма смыло следующую цифру, и номер стал четвертой
степенью целого числа. Какой номер мог быть на шхуне?
N2. Рассмотрим все параболы y = x2 + px + q,
пересекающие ось абсцисс в двух точках. Через три точки пересечения каждой параболы с осями координат
проведем окружность. Докажите, что на координатной плоскости существует точка, принадлежащая всем проведенным окружностям.
N3. В летней математической школе на веранде корпуса было выставлено 10
различных пар ботинок. Щенок, играя, утащил 4 ботинка. Какова вероятность того, что
среди украденных будет хотя бы два ботинка из одной пары?
N4. Треугольник АВС вписан в окружность и еще проведена
окружность через середины его сторон. Рассмотрим третью окружность, которая касается
описанной окружности в точке А и касается второй окружности внешним образом в
точке А1. Аналогично определяются точки В1 и С1.
Докажите, что прямые АА1, ВВ1 и СС1 пересекаются в одной точке.
N5. Докажите, что при a > 1 выполняется неравенство: 8(a – 1)2
+ (6 + 4a – 10a2)lna + (3a2 + 4a + 1)ln2a > 0.
II. Методическая часть.
В предложенных текстах (NN6 – 8) могут содержаться математические ошибки
(как в утверждениях, так и в ответах, решениях или доказательствах). Если утверждение неверно — приведите
контрпример и найдите ошибки в доказательстве. Если неверно только решение (доказательство) — укажите ошибки и приведите верное решение (доказательство).
N6. "Задача". Известно, что
x + y + z = a и x–1 + y–1 + z–1 =
a–1. Какие значения может принимать выражение (x – a)(y – a)(z – a)?
"Ответ": 0.
"Решение". Из второго равенства следует, что (xy + yz + xz)a = xyz.
Пусть xy + yz +zx = b. Тогда, используя теорему Виета,
получим, что x, y и z — корни уравнения t3 – at2 +
bt – ba = 0. Полученное уравнение можно записать в виде:
(t2 + b)(t – a) = 0, тогда одним из корней этого уравнения является число a.
Следовательно, хотя бы один из множителей искомого произведения равен нулю.
N7. "Задача". Найдите геометрическое место точек пространства, равноудаленных от двух скрещивающихся прямых. 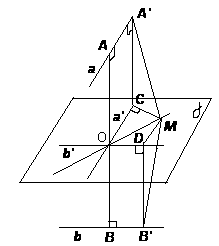
"Решение". Пусть прямые а и b — скрещиваются. Построим отрезок АВ — их общий перпендикуляр и плоскость 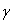 ,
перпендикулярную АВ и проходящую через точку О — его середину (см. рис.). ,
перпендикулярную АВ и проходящую через точку О — его середину (см. рис.).
Пусть прямые a' и b' — ортогональные проекции прямых а и
b на плоскость 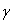 .
Тогда любая точка М, лежащая на биссектрисе углов, образованных прямыми a' и b',
равноудалена от прямых а и b. .
Тогда любая точка М, лежащая на биссектрисе углов, образованных прямыми a' и b',
равноудалена от прямых а и b.
Действительно, пусть MC и MD — перпендикуляры,
опущенные из точки М на прямые a' и b' соответственно, A' и B' —
ортогональные проекции точек С и D на прямые а и b.
Тогда A'M перпендикулярен a' и B'M перпендикулярен
b' (по теореме о трех перпендикулярах), значит, A'M перпендикулярен a
и B'M перпендикулярен b.
Кроме того, прямоугольные треугольники A'МC и B'MD равны (по двум катетам), поэтому A'M = B'M.
Если точка М не принадлежит ни одной из биссектрис указанных углов, то она не равноудалена от сторон угла, следовательно, не равноудалена от прямых а и b (если CM не равен
DM, A'C = B'D, то A'M не равен
B'M).
Таким образом, искомое ГМТ — две перпендикулярные прямые, лежащие в плоскости 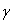 . .
N8. "Теорема". Пусть h(x) = f(g(x)). Тогда, если существует
g'(x0) и существует
f'(t0), где t0 = g(x0), то существует
h'(x0) = f'(g(x0))g'(x0).
"Доказательство". Рассмотрим 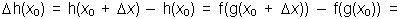 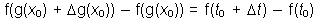 .
Кроме того, функция g(x) дифференцируема в точке x0, поэтому непрерывна в ней, следовательно, .
Кроме того, функция g(x) дифференцируема в точке x0, поэтому непрерывна в ней, следовательно, 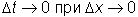 . .
h'(x0) = 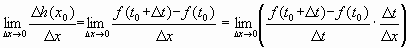 = =
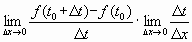 = = 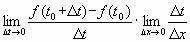 = =
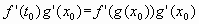 . .
N9. В различных школьных учебниках последовательность
изучения тем различна. Например, в учебнике геометрии А.В. Погорелова разделы
"Декартовы координаты на плоскости", "Движения" и "Векторы" изучаются в конце 8 класса
(именно в таком порядке), а "Площади фигур" — в конце 9 класса. В учебнике
Л.С. Атанасяна тема "Площадь" — в середине 8 класса, "Векторы" — в конце 8 класса,
"Метод координат" — в начале 9 класса, "Движения" — в конце 9 класса.
С методической точки зрения оцените "плюсы и минусы"
каждой из этих систем изложения геометрического материала.
|